1 (12) (123) (1234) ·· (12···100) I'll get one more term 1 (12) (123) (1234) (12 Ex 94, 1 Deleted for CBSE Board 22 Exams Ex 94, 2 Deleted for CBSE Board 22 Exams Ex 94, 3 Deleted for CBSE Board 22 Exams Ex 944 Important Deleted for CBSE Board 22 Exams You are here Ex 94, 5 Deleted for CBSE Board 22 Exams For the series S = 1 (1/(1 3))(1 2)2 (1/(1 3 5)) (1 2 3)2 (1/(1 of first 10 terms is 505/4 (D) sum of first 10 term is 405/4

Prove That 1 3n 2 1 3n 1 1 3n 1 3n For N Chegg Com
1/2 + 1/3 + 1/4 series
1/2 + 1/3 + 1/4 series-McCartney 3,2,1 With Paul McCartney, Rick Rubin 21 Six Episode Series on Hulu Producer Rick Rubin interviews Paul McCartney on his work with the Beatles, Wings, and as a solo artist, including stories about his personal relationships that inspired his songwritingSo e = 1 1 1 2!




Find The Sum Of The Series 1 3 2 5 4 7 8 9 16 Oo
Decimals (decimal numbers) enter with a decimal point and they are automatically converted to fractions ie 145 The colon and slash / is the symbol of division Can be used to divide mixed numbers 1 2/3 4 3/8 or can be used for write complex fractions ie 1/2 1/3 An asterisk * or × is the symbol for multiplication Let's do a couple of examples using this shorthand method for doing index shifts Example 1 Perform the following index shifts Write ∞ ∑ n=1arn−1 ∑ n = 1 ∞ a r n − 1 as a series that starts at n =0 n = 0 Write ∞ ∑ n=1 n2 1 −3n1 ∑ n = 1 ∞ n 2 1 − 3 n 1 as a series that starts at n =3 n = 3The idea becomes clearer by considering the general series 1 − 2x 3x 2 − 4x 3 5x 4 − 6x 5 &c that arises while expanding the expression 1 ⁄ (1x) 2, which this series is indeed equal to after we set x = 1
Liberty Pumps 253 1/3Horse Power 11/2Inch Discharge 250Series Cast Iron Automatic Submersible Sump/Effluent Pump 48 out of 5 stars 41 $ $ 179 25 The series mentioned above is in the form of GP (geometric progression) So the next term is 1/8 when we divide second term and first term we get a difference of 1/2 which is common throughout the seriesSeries 6 44mm or 40mm case size AlwaysOn Retina display GPS Cellular 1 1 8 7 4 6 GPS Blood Oxygen app 2 2 1 6 10 5 ECG app 3 3 2 7 11 6 High and low heart rate notifications Irregular heart rhythm notification 4 4 3 12 7 Supports Family Setup 10 5 5 11 8 (GPS Cellular models) Water resistant 50 meters 6 6 11 1 * Buy
Amygdala (1) Auditory Cortex (1) Basal Ganglia (2) Brainstem (2) Cerebellum (2) Corpus Callosum (1) Cranial Nerves (1) Frontal Lobe (3) Hippocampus (1) Hypothalamus (1) Limbic System (1) Meninges (1) Occipital Lobe (3) Olfactory Bulb (1) Parietal Lobe (2) Pituitary Gland (1) Prefrontal Cortex (1) Somatosensory Cortex (4) Spinal Cord (5Show work By signing up, you'll get thousands of stepbystep solutions to your homework questions You can= X1 n=0 17n n n!




Convergence Of Series 1 1 1 2 1 3 1 4 Ln 2 Alt Harmonic Ln 2 Youtube




Prove That 1 3n 2 1 3n 1 1 3n 1 3n For N Chegg Com
Find Friends The Complete Series Collection Seasons 1,2,3,4,5,6,7,8,9 & 10 DVD at Amazoncom Movies & TV, home of thousands of titles on DVD and Bluray Series such as 11/21/41/8 are called absolutely convergent series Rearrange the terms of an absolutely convergent series and you always get the same sum Different arrangements of the terms of a conditionally convergent series (one that is not absolutely convergent) can yield different sums Program to find sum of series 1 1/2 1/3 1/4 1/n If inverse of , 1/ (a d), 1/ (a 2d), 1/ (a 3d) 1/ (a nd) where "a" is the 1st term of




1 2 1 4 1 8 1 16 Wikipedia




Stolz Cesaro Theorem Online Presentation
X 2R cosx = 1 x2 2!What could we mean by the sum of the series X∞ k=1 1 2k = 1 2 1 4 1 8 = ?318 Chapter 4 Fourier Series and Integrals Zero comes quickly if we integrate cosmxdx = sinmx m π 0 =0−0 So we use this Product of sines sinnx sinkx= 1 2 cos(n−k)x− 1 2 cos(nk)x (4) Integrating cosmx with m = n−k and m = nk proves orthogonality of the sines




The Sum Of The Series 1 2 1 3 1 4 Upto Infinity Is 1 E 2 2 E 1 3 E 1 2 4 E 1 2




Consider The Conditionally Convergent Series Chegg Com
1 – 1/2 1/3 – 1/4 = 0 Before explaining how something can be equal to nothing, let me know explain how this bit of mathematics cropped up in the episode In order to raise funds to rebuild the church, Apu teaches the congregation to card count;28 For n ≥ 3, the function f(n) = 1 2 n3 − 5 is positive;The remaining part is easy Just notice that ζ ( 2) = ∑ n ≥ 1 1 n 2 = ∑ k ≥ 0 1 ( 2 k 1) 2 ∑ k ≥ 1 1 ( 2 k) 2 = π 2 8 ζ ( 2) 4, hence 3 4 ζ ( 2) = π 2 8 gives ζ ( 2) = π 2 6 as wanted Share answered Sep 15 '15 at 2341 Jack D'Aurizio



What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora




How To Solve Fraction Questions In Math 10 Steps With Pictures
Don't stop learning now Get hold of all the important mathematical concepts for competitive programming with the Essential Maths for CP Course at a studentfriendly price To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation CourseSequences and series are most useful when there is a formula for their terms For instance, if the formula for the terms a n of a sequence is defined as "a n = 2n 3", then you can find the value of any term by plugging the value of n into the formula For instance, a 8 = 2(8) 3 = 16 3 = 19In words, "a n = 2n 3" can be read as "the nth term is given by twoenn plus three" But since ∑ 1 / ( 2 n) = ( 1 / 2) ∑ 1 / n, theorem 1122 implies that it does indeed diverge For reference we summarize the comparison test in a theorem Theorem 1155 Suppose that a n and b n are nonnegative for all n and that a n ≤ b n when n ≥ N, for some N If ∑ n = 0 ∞ b n converges, so does ∑ n = 0 ∞ a n
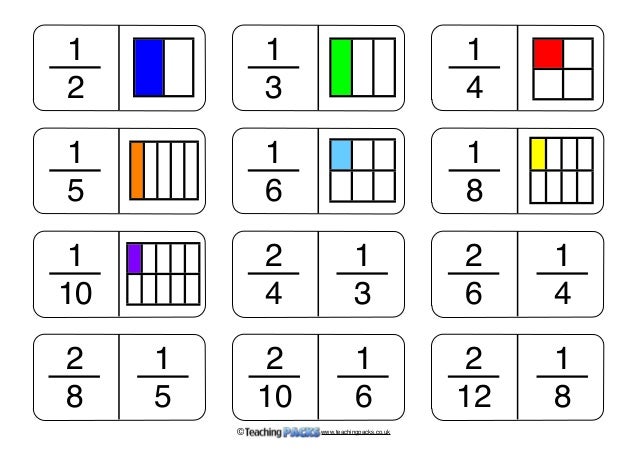



The Fractions Pack




A Oeis
N¡1=c 1c2¢2(x¡a)c3¢3(x¡a) 2c 4¢4(x¡a) 3 (4) Setting x =a;McCartney 3, 2, 1 Paul McCartney sits down for a rare indepth one on one with Rick Rubin to discuss his groundbreaking work with The Beatles, the emblematic 70s arenarock of Wings, and his 50 years and counting as a solo artist, in this sixepisode series that explores music and creativity in a unique and revelatory manner4 P 1 n=1 n2 41 Answer Let a n = n2=(n4 1) Since n4 1 >n4, we have 1 n41 < 1 n4, so a n = n 2 n4 1 n n4 1 n2 therefore 0




Java Program To Find Sum Of Harmonic Series 1 1 2 1 3 1 4 1 5 1 N The Crazy Programmer




Find The Sum Of The Series 1 3 2 5 4 7 8 9 16 Oo
Commonly Used Taylor Series series when is valid/true 1 1 x = 1 x x2 x3 x4 note this is the geometric series just think of x as r = X1 n=0 xn x 2( 1;1) ex = 1 x x2 2!Miranda and Max travel into wine country to investigate the killing of a dog at one of Mallorca's most famous vineyards, just one of an increasingly dramatic series of threats faced by property owner Hans Webber Add Image S1, Ep6 25 Nov 19 To Kill a StagAnswer to What is (2 1/2)/(1 1/4)?



The Ramanujan Summation And Others By Vishnu Vusirikala Nerd For Tech Medium



Arsenal Second Formation 4 2 1 2 1 Or 4 2 1 3 4 2 3 1 Football Tactics And Formations Sharemytactics Com
F′(n) = 3 2 n2 is positive and f(3) = 27 2 − 5 > 0 Adding 1 2 n3 to both sides of the inequality 0 < 1 2 n3 − 5 yields 1 2 n3 < n3 − 5 which implies 1 n3 − 5 < 2 n3 for n ≥ 3 Since P 2n−3 converges (it's a pseries with p = 3 > 1 So, I was wrong 1234 and 1/12 have a relationship with each other but certainly don't equal each other (Update 2614 that is, the series doesn't converge to 1/12, but I am still intrigued by the possibility, suggested by the Numberphiles, that it truly equals 1/12 if ALL the terms out to infinity are included in the sumA strategy that allows a player to beat the casino at blackjack




Examples 3 5 4 5 2 3 5 8 1 2 3 2 5 7 1 3 4 7 8 2 5 1 3 2 5 6 4 X 6 7 2 3 X 9 16 1 2 3 X 3 4 5 4 5 6 7 Ppt Download



What Is 1 4 2 3
In mathematics, 1 2 4 8 ⋯ is the infinite series whose terms are the successive powers of twoAs a geometric series, it is characterized by its first term, 1, and its common ratio, 2As a series of real numbers it diverges to infinity, so in the usual sense it has no sumIn a much broader sense, the series is associated with another value besides ∞, namely −1, 3 Take the first derivative of the resultant function to get back to the original function Then, we should have achieved the power series for 1/ (1x)^3 We get 1 Divide by 2 color (highlight) (1/2)* 1 x x^2 x^3 x^4 x^5 = 1/2 sum_ (n=0)^N (x)^n = 1/2 x/2 x^2/2 x^3/2 x^4/2 x^5/2E(17x) = P 1 n=0 (17 x)n!



Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot
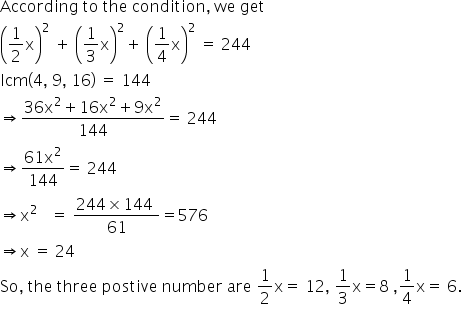



Three Positive Numbers Are In The Ratio 1 2 1 3 1 4find The Numbers Of The Sum Of Their Squares Is 244 Mathematics Topperlearning Com Kxsliw11
Here, a = 1/2 and r = 1/2 Therefore, the sum to infinity is 05/05 = 1 So every time you add another term to the above sequence, the result gets closer and closer to 1You can put this solution on YOUR website! #= 1^2 2^2 3^2 The #N# th term would be given by #(1)^(N1)N^2# , and the finite sum at the #N# th term would be found as follows If this series were not alternating, the sum would have been




1 2 1 4 1 8 1 16 Wikipedia




1 2 3 4 Wikipedia
In this tutorial, we can learn C program to sum the series 11/2 1/3 1/n In this c program, we enter a number and and generate the sum of series= X1 n=0 xn n!The nth Taylor Polynomial for sinx for x near a = 0 First calculate the derivatives of sin x!You should



Ragged Tensors Tensorflow Core



Rational Trees And Binary Partitions
In order to find the value of this series, we consider the related power series mathS(x) = \displaystyle \sum_{n=1}^{\infty} \frac{x^n}{n} \tag*{}/math Observe2 SOLUTION SET III FOR –FALL 04 Since the series in parenthesis is absolutely convergent (by the same criterion used to prove the absolute convergence of the Taylor series of ez and cosh z) we can divide by z2 both terms of the above equalityChapter 4 Taylor Series 18 45 Important examples The 8th Taylor Polynomial for ex for x near a = 0 ex ≈ P 8 = 1 x x2 2!




Schwarz Schrumpfschlauch 1mm 50mm 2 1 3 1 4 1 Auto Draht Kabel Elektrisch Diy Ebay




Wolfram Alpha Examples Step By Step Solutions
22 Examples Power Series Expansion of ln(1x) Note d dx ln(1x) = 1 1x = X∞ k=0 (−1)kxk for x < 1 Integration ln(1x) = X∞ k=0 (−1)k k 1 xk1(C = 0) = X∞ k=1 (−1)k k xk = x− 1 2 x2 1 3 x3 − 1 4 x4 ··The interval of convergence is (−1,1 At x = 1, ln2 = X∞ k=1 (−1)k k = 1− 1 2 1 3 − 1 4 Show Solution To determine if the series is convergent we first need to get our hands on a formula for the general term in the sequence of partial sums s n = n ∑ i = 1 i s n = ∑ i = 1 n i This is a known series and its value can be shown to be, s n = n ∑ i = 1 i = n ( n 1) 2 s n = ∑ i = 1 n i = n ( n 1) 2Provides worked examples of typical introductory exercises involving sequences and series Demonstrates how to find the value of a term from a rule, how to expand a series, how to convert a series to sigma notation, and how to evaluate a recursive sequence Shows how factorials and powers of –1 can come into play



Haubenverriegelung Grosssegler 1 2 1 3 1 4 In Hessen Wettenberg Ebay Kleinanzeigen




Express In Simplest Form 1 2 1 3 1 4 Brainly In
11 Sequences and Series Consider the following sum 1 2 1 4 1 8 1 16 ··· 1 2i The dots at the end indicate that the sum goes on forever Does this make sense?We have f0(a)=c 1 We repeat the same process again and again take derivative again on (4) f00(x)= X1 n=2 cnn(n¡1)(x¡a) n¡2=c 2¢2¢1c3¢3¢2(x¡a)c4¢4¢3(x¡a) 2 (5) 5Elite wep series review in Teluguseason 1season 2season 3season 4Telugu review




What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora



The Value Of The Sum 1 3 2 1 1 4 2 2 1 5 2 3 1 6 2 4 Is Equal To Sarthaks Econnect Largest Online Education Community
Output 2 Attention reader! Ex 94, 1 Deleted for CBSE Board 22 Exams You are here Ex 94, 2 Deleted for CBSE Board 22 Exams Ex 94, 3 Deleted for CBSE Board 22 Exams Ex 944 Important Deleted for CBSE Board 22 Exams Ex 94, 5 Deleted for CBSE Board 22 ExamsThe number that doesn't belong to this series 1, 1, 2, 3, 4, 5, 8, 13, 21 is 4 A series is a set of numbers following a pattern Answer The number 4 does not




Write Down The Next 3 Numbers In Each Sequence 1 2 4 6 8 10 2 1 3 5 7 9 3 1 4 9 16 25 36 4 1 2 1 3 1 4 5 1 Ppt Download



Q Tbn And9gcqu8faeki7cypmf8hq56iqys Li9ev6fccwfo0eyp86m5fli1 Usqp Cau
Let us try adding up the first few terms and see what happens If we add up the first two terms we get 1 2 1 4 = 3 4 The sum of the first three terms is 1 2 1 4 1 8 = 7 8 The sum of the first four terms is 1 2 1 4 1 8 1 16 = 15 16 And the sumFibonacci Sequence The Fibonacci Sequence is the series of numbers 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, The next number is found by adding up the two numbers before it1 1 3 ⋯ 1 2 k − 1 − 1 2 1 2 k 1 ⋯ 1 2 j 1 > 100 1 1 3 ⋯ 1 2 k − 1 − 1 2 1 2 k 1 ⋯ 1 2 j 1 > 100 Then subtract 1 / 4 1 / 4 Continuing in this way, we have found a way of rearranging the terms in the alternating harmonic series so that the sequence of partial sums for the rearranged series is




Infinite Series 4 4 14 We Now Study A Discrete Analogue Of Improper Integrals In Which We Asked If The Areas Represented By Integrals Of Unbounded Ppt Download



1



2




C Exercises Find The Sum Of The Series 1 1 2 2 1 3 3 1 N N W3resource
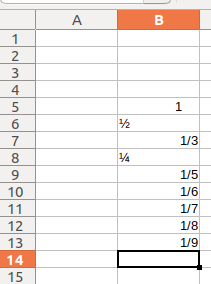



Could Not Insert Fractions 1 2 1 4 English Ask Libreoffice




Prove The Following By Using The Principle Of Mathematical Induction For All N N 1 3 1 1 5 4 1 7 9 1 2n 1 N 2 N 1 2 Mathematics Shaalaa Com




Evaluating The Nested Radical Sqrt 1 2 Sqrt 1 3 Sqrt 1 Cdots Mathematics Stack Exchange




Top Eleven Forum



Adding And Subtracting Fractions Ppt Download




Bruch Rechner Zoll Cm Tabellen Mit Umrechnung Bruche Wie 1 2 1 3 1 4 2 3 3 4 3 8 Zoll Nach Cm Mm µm Dezimal Etikettenvorlagen Tabelle Anleitungen




Copterlabel Eu Flugzeugkennung Aufkleber Massstab 1 2 1 2 5 1 3 1 3 5 1 4 1 5




Find The Sum To N Terms Of The Series 1 2 3 2 5 2 To N Terms




Ex 9 4 4 Find Sum Of Series 1 1 X 2 1 2 X 3 1 3 X 4




The Relations R 1 4 2 2 3 2 3 3 Chegg Com




Fraction Half Quarter Fourth Fractions 1 2 1 3 1 4 Half Quarter Fourth Vector Illustration Canstock




How T 2 1 3 5 7 2 4 6 8 Come Mathematics Stack Exchange



Fractions Cut And Paste Sort Activity 1 2 1 3 1 4 2 3 3 4 King Virtue



How Does One Calculate The Sum Math Frac 1 2 3 Frac 1 3 4 Frac 1 4 5 Frac 1 48 49 Frac 1 49 50 Math Quora



What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora




Unbekannt Englisch Baby Rattle Mit Beissring 1921 Silber Elfenbein 3 1 4 X 2 1 8 X 1 2 In 8 3 X 5 4 X 1 3 Cm Stockfotografie Alamy




Paradox 1 1 2 1 3 1 4 0 The Simpsons And Their Mathematical Secrets




Gn Behalter Gastronorm Deckel Silikondichtung 1 1 1 2 1 3 1 4 1 6 2 3 Edelstahl Ebay



What Is 1 3 1 4




Gn Behalter 65mm Grossen Auswahl Gn 1 2 1 3 1 4 2 3 Gastronormbehalter Chafing Warmhaltebehalter Gn 1 2 65mm Amazon De Kuche Haushalt Wohnen




Ex 4 1 11 Prove 1 1 2 3 1 2 3 4 1 3 4 5 1 N N 1 N 2




Fraction Circles 11 Worksheets 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 10 1 11 1 12 Halves Thirds Forths Fifths Sixths S Fractions Fraction Circles Worksheetfun



Fractions Cut And Paste Sort Activity 1 2 1 3 1 4 2 3 3 4 King Virtue




Dividing Fractions Using Fraction Strips Understood For Learning And Thinking Differences
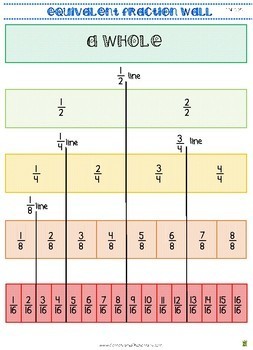



Fraction Wall Anchor Chart Poster 1 2 1 3 1 4 1 5 1 6 To 1 4 N F 1




Einheitsanteile Die Als Teile Eines Quadrats Gezeichnet Sind Einer Von Den Ersten Sechs Machten Von Zwei Geteilt Erste Sechs Summanden Der Unendlichen Serie 1 2 1 3 1 4 1 8 1 16 1 64 Schwarz Weiss Illustration Vektor
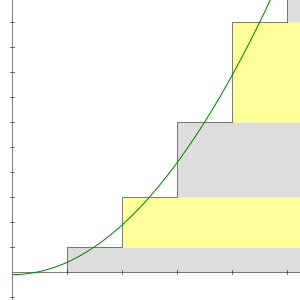



1 2 3 4 Wikipedia




The Sum Of The First 35 Terms Of The Series 1 2 1 3 1 4 1 2 1 3 1 4 1 2 1 3 1 4 Is 1 2 B 1 4 C 1 4 E None Of These




Pizza Fraction Bingo 1 2 1 3 1 4 1 5 Teaching Resource Teach Starter




How To Find 1 2 1 4 1 8 Video Lesson Transcript Study Com




Harmonic Series Mathematics Wikipedia




Mcr 3u Sequences And Series Test 2




Ex 9 4 4 Find Sum Of Series 1 1 X 2 1 2 X 3 1 3 X 4
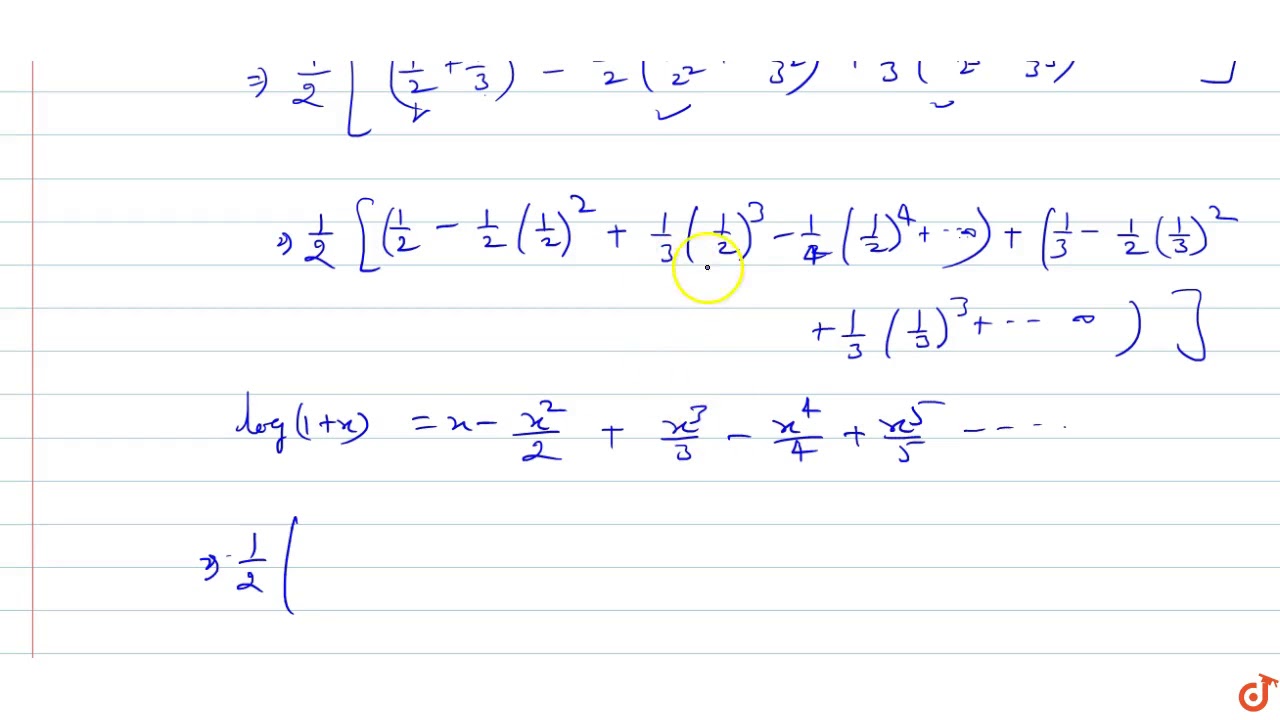



Sum Of The Series 1 2 1 2 1 3 1 4 1 2 2 1 3 2 1 6 1 2 3 1 3 3 Oo Youtube




Yato Profi Polycarbonat Gn Abtropfgitter Fur Gastronormbehalter 1 1 1 2 1 3 1 4 1 6 Grossen Auswahl Gastro Norm Kunststoff Drainage Abtropf Gitter Einlege Boden Ablauf Gn 1 4 Amazon De Gewerbe Industrie Wissenschaft



Natural Numbers Series 8 Sideway Output To




Why Does The Series Sum N 1 Infty Frac1n Not Converge Mathematics Stack Exchange
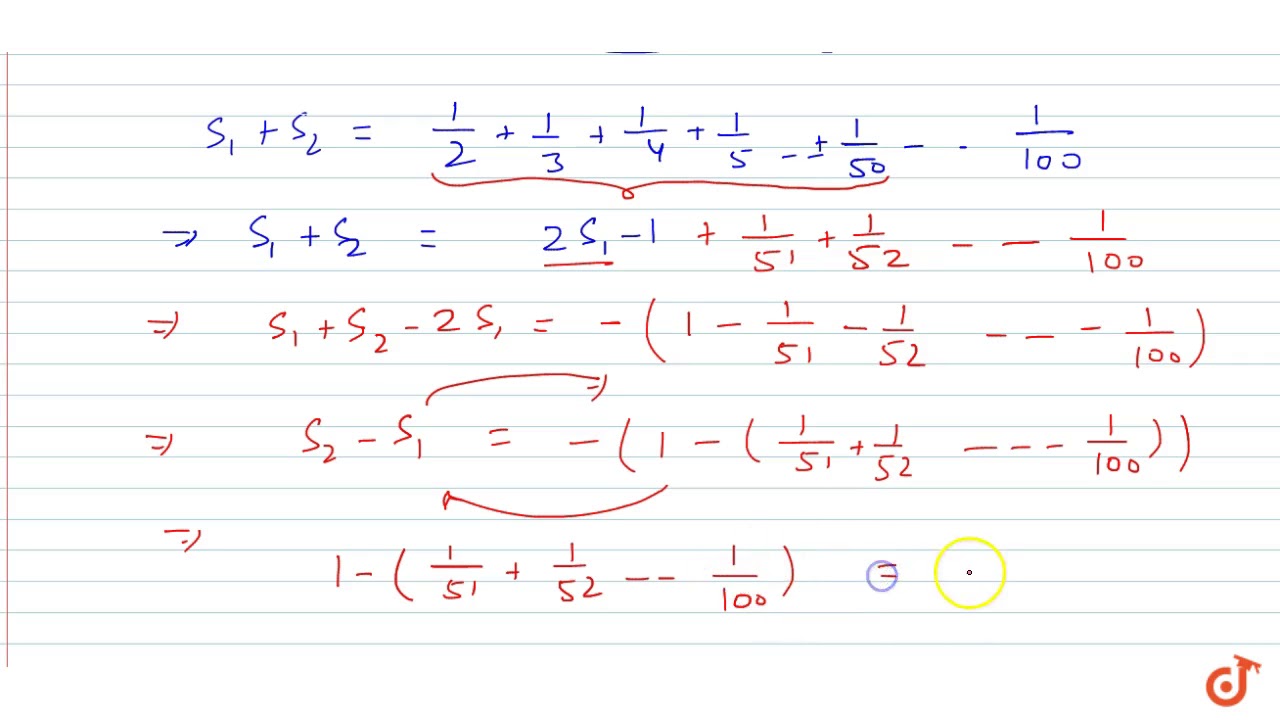



Prove That 1 2 1 3 1 4 1 5 1 98 1 99 1 100 Gt1 5 Youtube
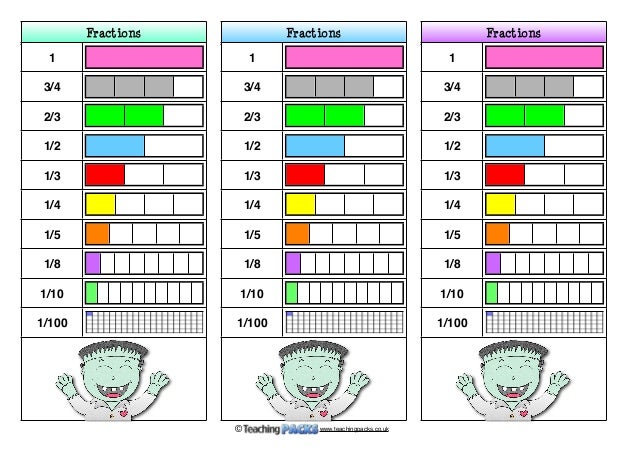



The Fractions Pack



Find The Sum Up To N Terms Of The Given Series 1 1 1 2 1 4 2 1 2 2 2 4 3 1 3 2 3 4 N Sarthaks Econnect Largest Online Education Community




1 2 3 4 Wikipedia




C Program To Print Sum Of Series 1 1 1 2 1 3 1 N Quick Solution




Solve 1 2 1 3 1 4 1 5 1 6 Brainly In




Calameo Tableau Des Complementaires




0 12 Smooth Shank Diamond Point Metal Dewalt Dwc12p1d Coil Framing Nail 3 1 4 L Round Head 3 1 4 L Fasteners Industrial Scientific Fcteutonia05 De
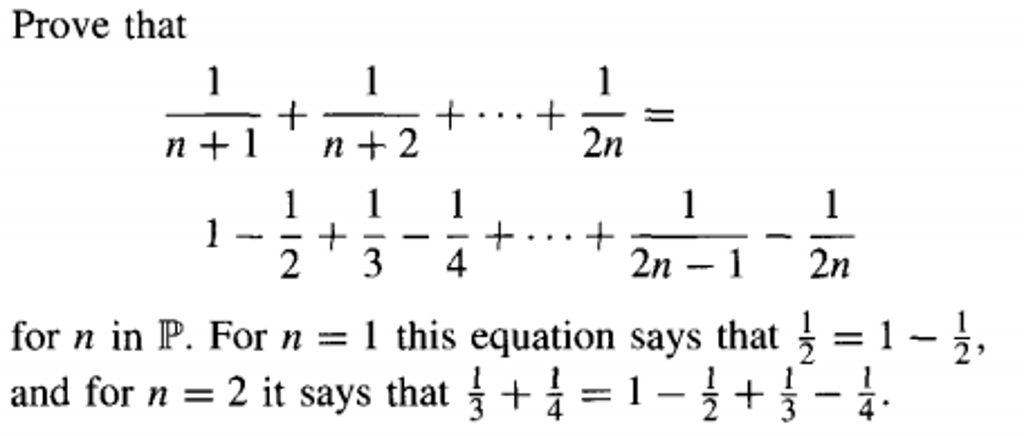



Prove That 1 N 1 1 N 2 1 2n 1 1 2 Chegg Com



How To Prove That 1 1 5 2 9 3 13 4 E 3 Quora




Solve 7 1 2 2 1 4 1 1 4 1 2 1 1 2 1 3 1 6 2 9 B 4 1 2 C 9 1 2 D 1 77 228



Q Tbn And9gcspugupatyyfeoe7gdnk6gwyu1 Awz34y5ydat9gedqskf6us7e Usqp Cau




How To Find The Sum Of The Series Math Frac 1 1 Cdot 2 Frac 1 2 Cdot 3 Frac 1 3 Cdot 4 Frac 1 4 Cdot 5 Ldots Frac 1 N N 1 Quora



Www Jstor Org Stable 10 4169 x




A Simple Proof That The Harmonic Series Diverges Math



Easy Fraction Snap Cards 1 2 1 3 2 3 1 4 2 4 3 4 Ks1 Or Ks2 Year 2 3 4 Teaching Resources




Sum Of The Series S 1 1 2 1 2 1 3 1 2 3 1 4 1 2 3 4 Upto Terms Is




How To Find The General Term Of Sequences Owlcation




Let F 1 2 3 4 2 3 1 4 G 1 2 3 4 1 3 4 2 Be Chegg Com
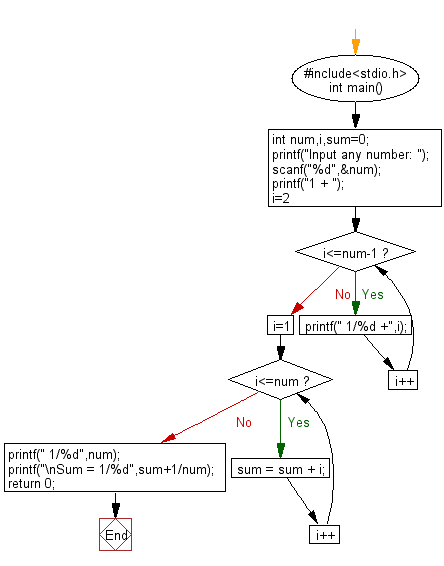



C Exercises Display Sum Of Series 1 1 2 1 3 1 N W3resource



Causality Fig 4 Causality Fig 5 Causality X1 1 0 1 0 X2 1 2 2 4 X3 1 Download Scientific Diagram




How To Solve The Following Equations 1 5 X 1 2 1 3 2 1 4 X 1 2 1 3 3 1 1 2 M 3 4 1 2 Socratic
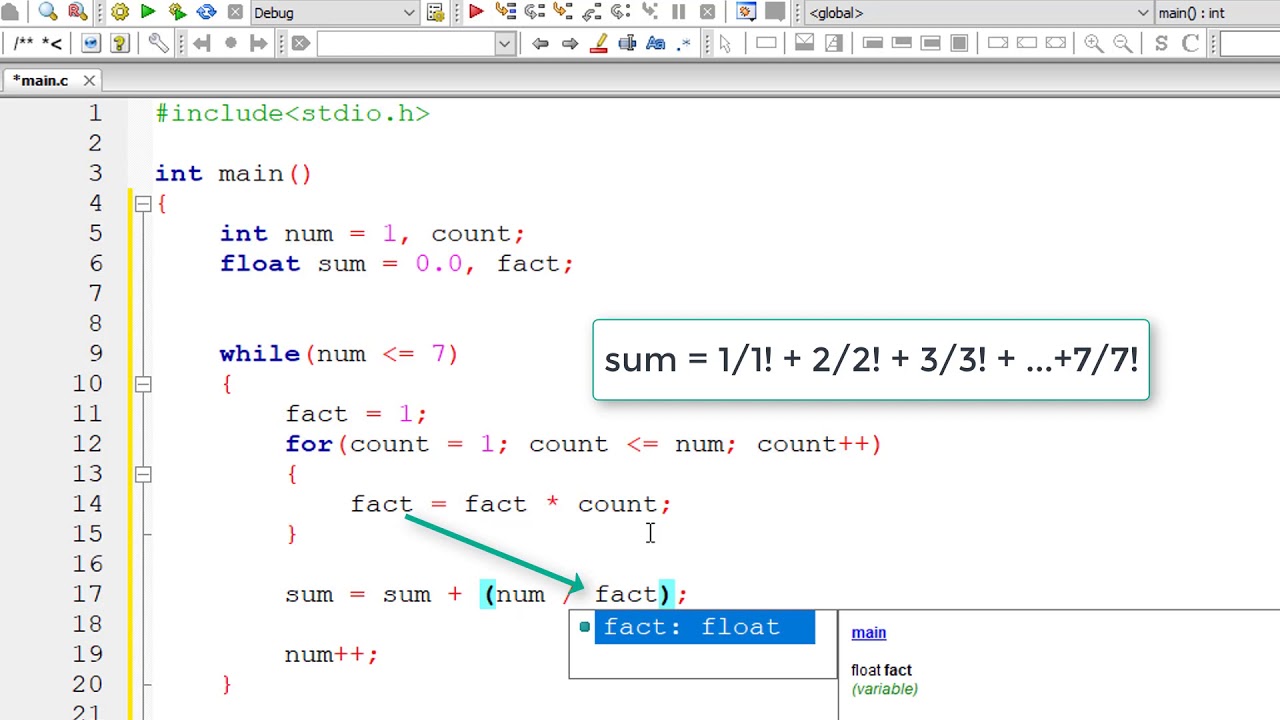



C Program To Find Sum Of Series 1 1 2 2 3 3 N N Youtube



1




1 2 1 3 1 4 Mathematics Topperlearning Com Psqpqtcc




Solve The Following 5 1 2 1 3 1 4 Mathematics Topperlearning Com 1lw16x22




1 1 1 3 1 2 1 4 1 5 1 4 1 6 Determine Whether The Sequence Converges Or Diverges Youtube
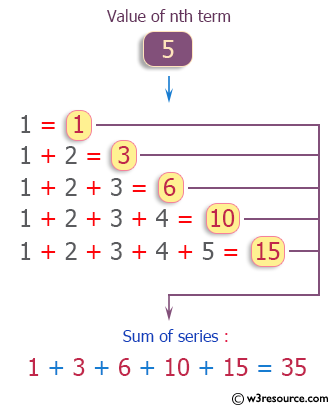



C Exercises Calculate The Series 1 1 2 1 2 3 1 2 3 4 1 2 3 4 N W3resource



What Is The Value Of The Product 1 1 2 1 1 3 1 1 4 1 1 5 Quora



1 2 3 4 Wikipedia




1 3 3 4 Football Tactics Formations




Ex 7 6 1 Solve A 2 3 1 7 B 3 10 7 15 C 4 9 2 7 D 5 7




Paradox 1 1 2 1 3 1 4 0 The Simpsons And Their Mathematical Secrets



0 件のコメント:
コメントを投稿