正八面体 正三角形 4 6 12 正十二面体 正五角形 3 30 正二十面体 正三角形 5 12 30 体積比と表面積比 編集 相似比が 四谷大塚 予習シリーズ のテキストは四谷大塚よりお買い求め下さい。A=面積 鋭角三角形 鈍角三角形 台 形 不平行四辺形 なお点線にて示すごとく二つの三角形となし、各々の面積を計算し、 その和をもって不平行四辺形の面積を算出してもよい。正 n 角形の面積は一辺を a とすると n a 2 4 cot π n {\displaystyle {na^{2} \over 4}\cot {\pi \over {n}}} と求められる。 この式は、正 n 角形の外心から、各頂点に向けて、線分を引き、 n 個の二等辺三角形に分割することで容易に証明できる。
腾讯视频
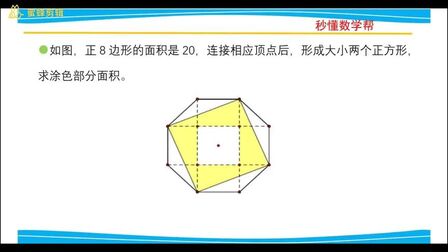
正八角形 面積 高校
正八角形 面積 高校-正六角形の面積比 (麻布中学 受験算数問題 09年) 正多角形の面積公式一覧と導出方法を解説正二十四角形まで 21年1月28日 1辺の長さaの正方形の面積は、もちろん a 2 ですが、正三角形の面積公式は知っていますか 中学や高校の試験で登場するため、正三角形の面積公式は覚えておいて損はありませ



这个正八边形面积挺好算 但是你有没有简单的方法是学问 哔哩哔哩 Bilibili
「正八 角形の面積が100cm2のとき,台形(左側の図)の 面積を求める問題」と答えていた。その問題の答 は,放映されなかったので,私なりに考えてみ た。右側の図より, hsg≡ posであるから,「(台形abgh)= 4 1 (正八角形abcdefgh)」と三角形の面積の 倍とします。すると,切断面Uの面積は①× ,正三角形LMNの面積は③× +(底 正三角形LMNは切断面Uの3倍よりも1辺の長さが1㎝の正三角形2個分だけ大きいということで す。正八 角形 面積。 八角形 (斜線部分の面積を求める問題です) また、新しいところでは昨年度の灘中(1日目9番)で という問題が出題されました。
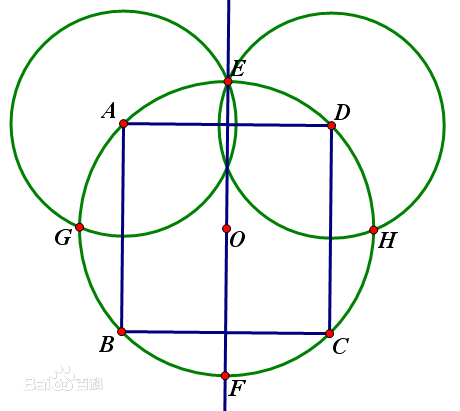
正多角形の面積 sqrt (xx) のように指定してください。 正多角形の1番長い対角線の長さを表示してほしい。 1辺を1としたときと仮定した時でいいので。 非常に役に立った。 立式できても計算に時間が取られていたが、こちらのサイトで瞬時に答えが出た また、円の面積より内接する正六角形の面積のほうが小さいので、円周率πは2より大きい$\left(\pi>2\right)$ことがわかります。 外接する正八角形 図2 円に外接する正八角形第47問 正方形と正八角形 図形ドリル 6年生 正八角形 正方形 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。
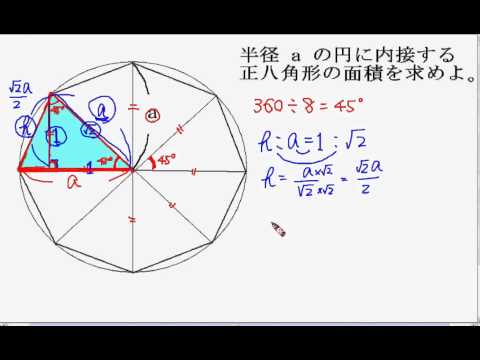
半径1の円に内接する正八角形の面積Sを求めよ。 という問題がわからないです、どなたか教 Clear 数学 高校生 2年以上前 ゲストさん 半径1の円に内接する正八角形の面積Sを求めよ。 という問題がわからないです、どなたか教えてください! 図形と計量① 正五角形 正六角形 正八角形 正十角形 ② ③ ④ 正多角形の1つの角=多角形の角の和÷角の数 今回は正八面体の表面積、体積等を求めていきす。 このあたりまでは高校レベルの数学で解けますね。 導出の都合上、今までと求める量の順番を変えてます。 幾何学的対象の個数等 内接球・辺に接する球・外接球の半径 表面積 体積 隣り合う2つの面のなす角 一辺の長さを とし、以下のよ




正八邊形 八條長度相等的線段 首尾相連構成的一個封閉形狀的平面圖形叫正八邊形 華人百科



八角形面積計算八角形面積公式 百度知道狀態 Ekcup
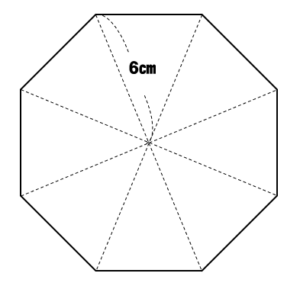
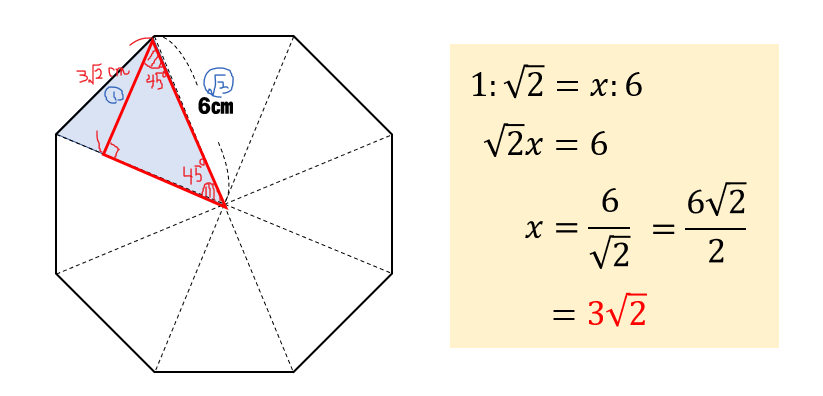
下の図1のような,面積が36cm2である正三角形2個を図2のように 重ねて,重なった部分が正六角形になるようにします。この正六角形の 面積を求めなさい。 図1 図2About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators一辺6cmの正八角形の面積を求めよ。 図のように補助線をひき、各点に記号をつけます。 正八角形の一つの内角は135°なので ∠HAK=90°、∠BAK=45°です。 よって AKBが直角二等辺三角形なので AB=6cm, AK=BK=3 2cm となります。




正八邊形中的等積變換 含原面積 Youtube




八边形对角线计算公式 正八边形边长计算 三人行教育网 Www 3rxing Org
これらは正八角形の周囲と一致することが分かります。 さて、 正八角形の面積 =四角形abcdbb 2 b 3 c =×8 =96cm 2 一方、正八角形の中心をoとすると、 oadは底辺がadで頂角(∠aop)が45度の二等辺三角形となるので、 padと合同。 よって、 pad=正八角形12cm 2正八角形面積求め方, 正多角形 正 n 角形の面積は一辺を a とすると n a 2 4 cot π n {\displaystyle {na^{2} \over 4}\cot {\pi \over {n}}} と求められる。 この式は、正 n 角形の外心から、各頂点に向けて、線分を引き、 n 個の二等辺三角形に分割することで容易に証明正多面体の思考の塗り分け ~ちょっと変えたn色問題~ ~ちょっと変えたn色問題~ 札幌藻岩高等学校 中村 文則 ついに~S先生がやってしまった! 見学旅行の引率でどっぷり疲れて職員室に辿り着くと,机の上にレポートが置かれていた.触ると



这个正八边形面积挺好算 但是你有没有简单的方法是学问 哔哩哔哩 Bilibili



一辺の長さが1の正八角形の面積の簡単な求め方を教えて下さい 答えでは余弦 Yahoo 知恵袋
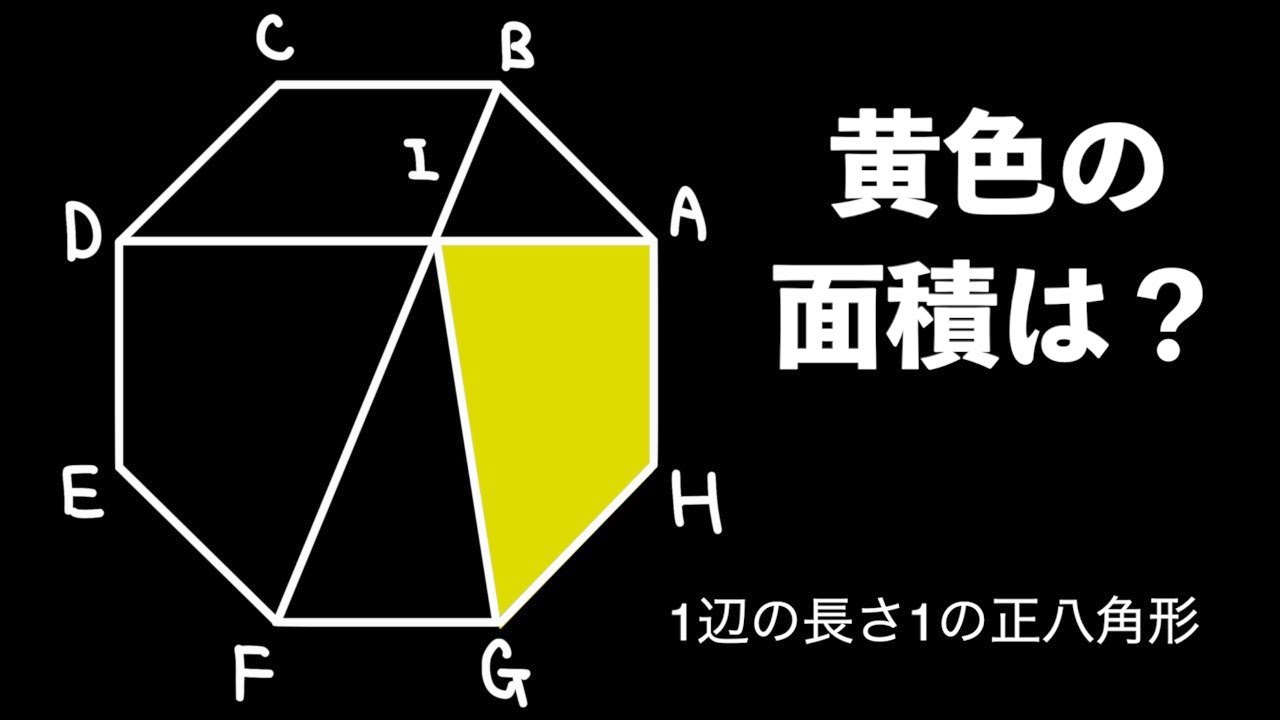
次の面積を求めよ。 (1)1辺の長さが1の正十二角形 (2)直径1の円に内接する正十二角形 分かりやすく教えてください。 数学 『正八角形の3点を結んでできる ABCの面積を1とする時、正八角形の面積はいくらになるか』という問題です。 答えの選択肢は5つ三平方の定理4 解説 1辺6cmの正八角形の面積を求めよ。 図のように補助線をひき、各点に記号をつける。 正八角形の一つの内角は 135°なので ∠HAK=90°、∠BAK=45°また、∠AKB=90°である。 すると AKBが直角二等辺三角形になるので AB=6cm, AK=BK=3 2 cmとなる(「正多角形の面積の公式」を参照) 今回は、正 \(~n~\) 角形の面積、つまり一般化してみたいと思います ;




H6vmzyyq9tktum



Math Reading Room八边形的面积 好简单 Math Reading Room
正八面体の表面積・体積・半径 正八面体 の表面積、体積そして半径(内接球と外接球)を求めてみましょう。 図1は 正八面体とそれに内接する内接球の図です。 表面積は簡単に計算できて、一辺の 長さが1の正三角形が八面あるので、(ルート3/4)X8 一辺の長さが1の正八角形の面積の簡単な求め方を教えて下さい。 答えでは余弦定理などを使っていました。ちなみに答えは2√22です。 下図のように、正八角形の1つおきの辺を延長して正方形pqrsを作ると、 pabは直角二ついて面積を求める。点Cから辺ODに下ろした垂 線の長さは5(三平方の定理, 1 2 p 3)であるから, OCDの面積S2 は, S2 = 10 5 1 2 = 25 正十二角形の面積はS2 の12 個分なので, この正十 二角形の面積St は, St = 25 12 = 300 同様に, 正方形の面積と円の面積の関係を示すと




一道有趣的面積求解問題 挑戰一下吧 每日頭條



趣题 圆内接八边形的面积 Matrix67 The Aha Moments
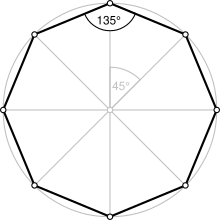
正八 角形 面積 Tassimo; 第46問 正八角形 図形ドリル 6年生 台形 正八角形 面積比 ★★★★★☆(算オリ・灘中受験生レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの図形問題を正八角形 においては、一つの 外角 と 中心角 は 45 ° で、 内角 は135°になる。 一辺の長さを a とすれば、周長は 8a 、面積 A は下記となる。



半径aの円に内接する正八角形の面積の答えを計算式とともにお願 Yahoo 知恵袋



正八邊形內三角形的面積 數學謎題 Gameschool遊戲學校
AOBの面積を求めて8倍すれば良いわけです。 解説 AOBの底辺はRで高さはhであるとし、 hをRで表すことを考える。 45゜ AOHはAH=OHの直角二等辺三角形である。 つまり、辺の比は そこで、 =h となる。 AOB = 2 /4 よって、求める8角形の面積は 2 = 2 2ひし形の面積の公式は 「たての対角線の半分の長さ」と「横の対角線の半分の長さ」の直角三角形の 4倍と考えると分かりやすいです。 ギャラリー 星形八角形 星形八角形(ほしがた はっかくけい)は、八角形を生み出す、あるいは、八角形が生み出す、形の構造をもった図形である。正三角形の面積から、1辺の長さ・面積を計算します。 面積Sが1の正三角形 1辺の長さ a: 高さ h:



1




八邊形面積八邊形 Nqnpg
その中に内接する正12角形の面積を考えました。 見通し 正12角形ですから、図の AOBと合同な二等辺三角形が12個あります。 AOBの面積を求めて12倍すれば良いわけです。 解説 AOBの底辺はRで高さはhであるとし、 1辺の長さが a の正三角形の面積は 1 2a2sin60 ∘ = √3 4 a2 で、確かに合ってますね。 正方形 (n = 4) S4 = 2R2 = a2 (a = √2R)八角形の周囲と面積を計算する方法 八角形の面積(対辺から) 面積計算機 高校数学Ⅰ「正多角形の面積の求め方」 映像 八角形の一辺の長さを求める公式を教えてくださ 12角形の面積 tokumathcom
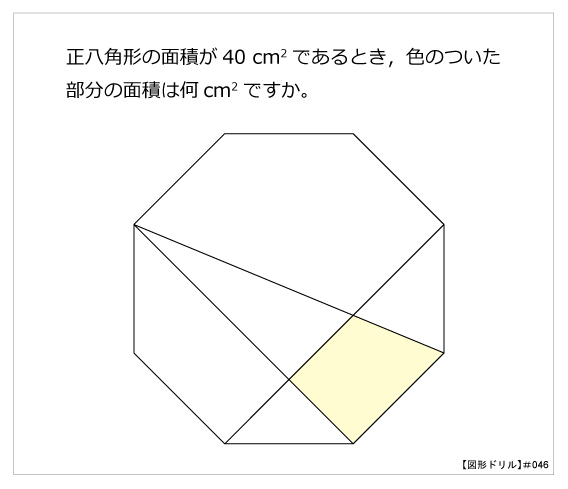



図形ドリル 第46問 正八角形 算数星人のweb問題集 中学受験算数の問題に挑戦




八边形 维基百科 自由的百科全书
正八面体は、その構成をしっかり把握してさえいれば、非常に取り組みやすい立体です。当初から伝え続けている通り、いかに「正多面体に慣れ親しんできたか」が効いてきます。 例えば、下記のような問題をスラスラ解けるか、チェックしてみましょう。 問題 1辺の長さが2の正八面八角形の内角の和は1080度である。 項目を8本の放射線に分けて、8つの項目の大小を対比する図表を、「オクタゴンチャート 要曖昧さ回避 」という。;正9角形の角度 正9角形の1つの角度(内角)は140°です。正9角形の内角の和=180°×(n-2)=180×(8-2)=1260°です。1260°÷9=140°になりますね。また、外角=180°-140°=40°です。 まとめ 今回は、正8角形(正八角形)の角度について説明しました。




如何找到八边形的面积 数学21




02正八边形的相关计算圆2 初中数学初三 Youtube




八角形の周囲と面積を計算する方法



八角形边长 万图壁纸网
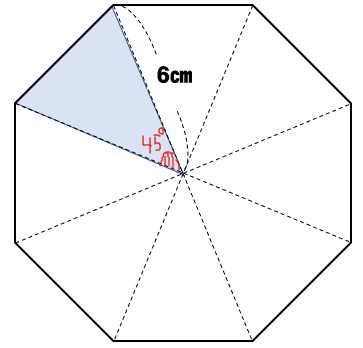



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ




八邊形面積八邊形 Nqnpg




八邊形面積 信欣茗數學園地 隨意窩xuite日誌




02正八边形的相关计算圆2 初中数学初三 Youtube
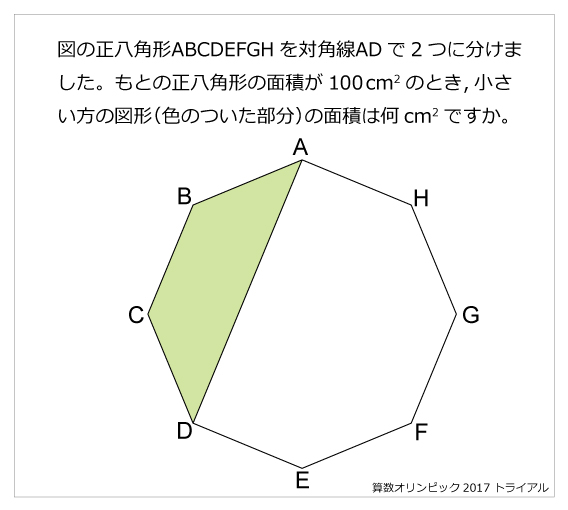



正八角形 算数星人のweb問題集 中学受験算数の問題に挑戦



1




八邊形 簡介 正八邊形 周長 面積 作圖 八邊形的套用 中文百科全書



8角形の面積




八角形の周囲と面積を計算する方法




六角形面積公式正六邊形 Utvos




図形ドリル 第47問 正方形と正八角形 算数星人のweb問題集 中学受験算数の問題に挑戦




六角形面積公式正六邊形 Utvos



請問是正八邊形嗎 雪花新闻




八边形 维基百科 自由的百科全书




求半徑為1 的圓外切正十邊形之邊長 信欣茗數學園地 隨意窩xuite日誌



腾讯视频



正八邊形內三角形的面積 數學謎題 Gameschool遊戲學校




八角形面積計算的影片 第1集 Youtube 線上影音下載




正八邊形 八條長度相等的線段 首尾相連構成的一個封閉形狀的平面圖形叫正八邊形 華人百科
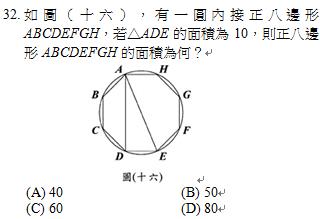



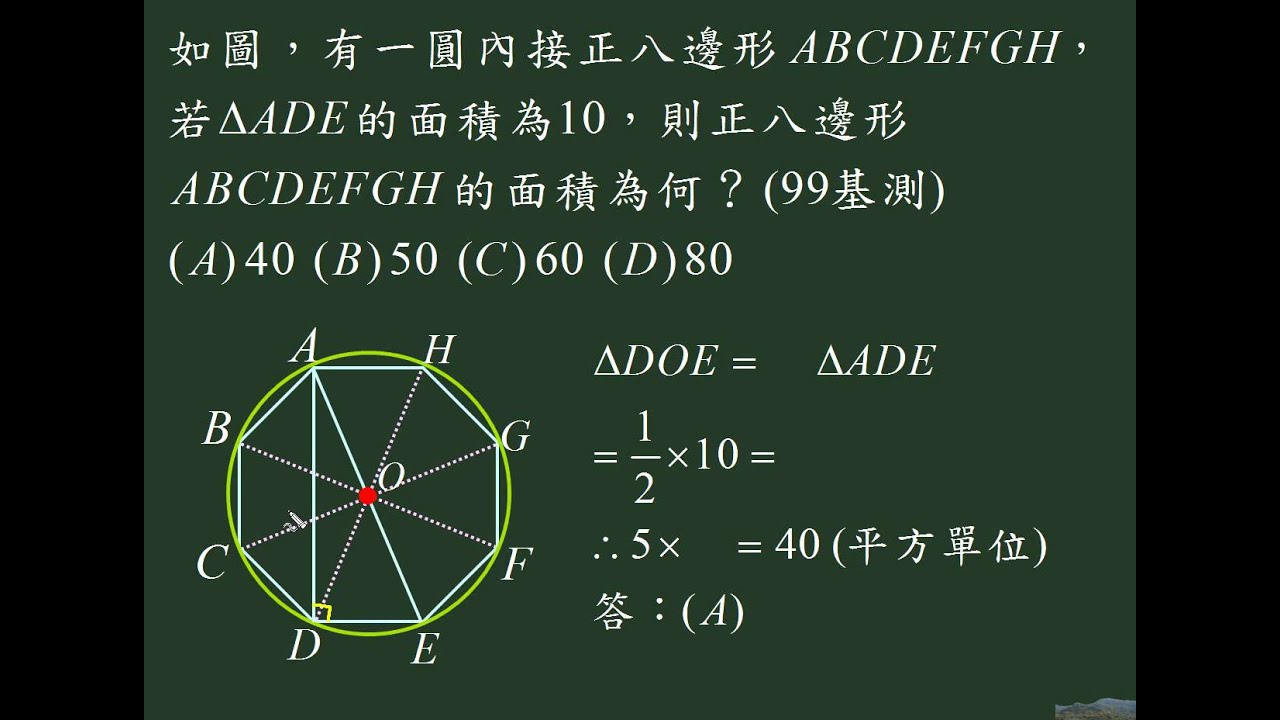
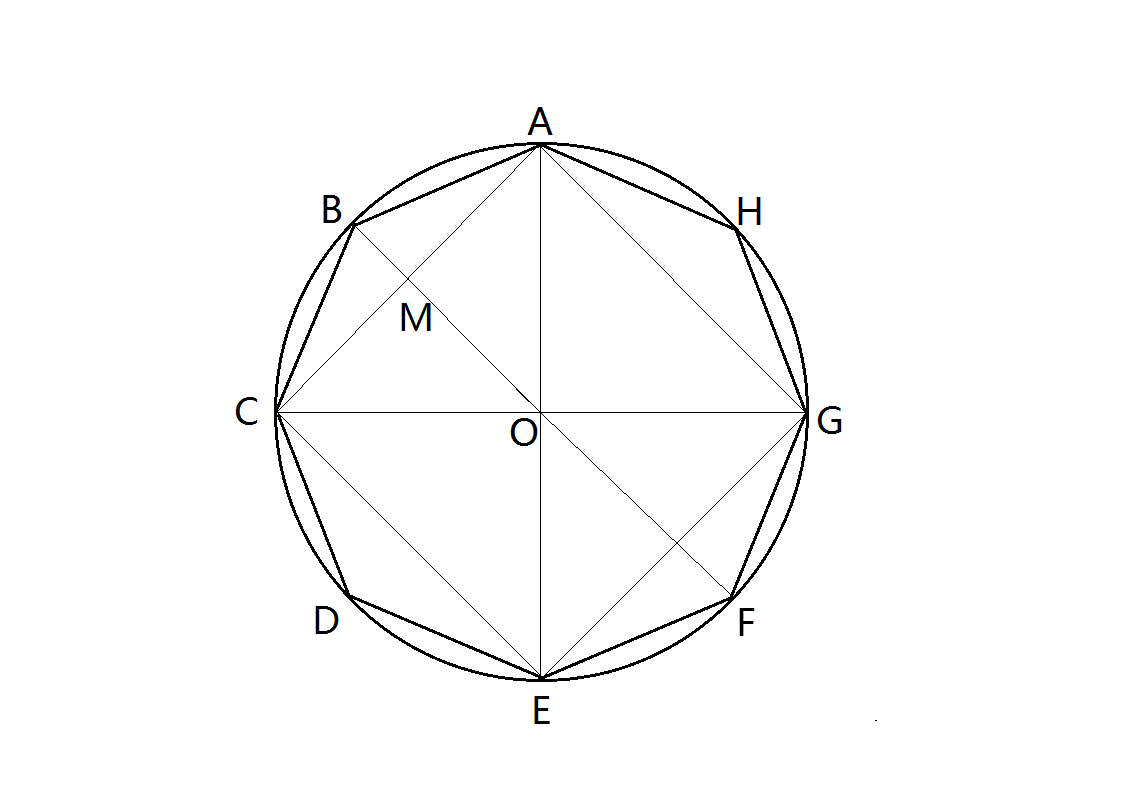
32 如圖 十六 有一圓內接正八邊形abcdefgh 若 Ade的面積為10 阿摩線上測驗




H6vmzyyq9tktum



正八邊形內三角形的面積 數學謎題 Gameschool遊戲學校



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ



内八角形怎么画 万图壁纸网




八边形怎么画图片第1页 驾考预约大全




六邊形 圖形 六邊形是多邊形的一種 指所有有六條邊和六隻角的多邊形 正 華人百科




八边形 全世界条目



正八邊形 Youtube



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ



八邊形 簡介 正八邊形 周長 面積 作圖 八邊形的套用 中文百科全書




正八边形 搜狗图片搜索



八邊形 簡介 正八邊形 周長 面積 作圖 八邊形的套用 中文百科全書



八邊形面積 信欣茗數學園地 隨意窩xuite日誌



Q Tbn And9gcr6br Oxol4soj8jhaap6e5yoavx9 Cepch0ccusgm Usqp Cau



八边形 维基百科 自由的百科全书




六边形 维基百科 自由的百科全书



中3数学 正八角形の面積 Youtube



八邊形的面積 數學謎題 Gameschool遊戲學校



正八角形の領域面積 Youtube



正八边形 西瓜视频搜索




數感實驗室numeracy Lab 數感教育 在數學世界裡活用數學 2 1 41 3 1 73 所以 2 3 1 41 1 73 3 14 修但幾咧 這不是圓周率嗎 換句話說 2 3 P 大哲學家卡爾 波普爾認為 是柏拉圖發明了這條件似式 柏拉圖甚至認為這不只是近似 而是




八边形 维基百科 自由的百科全书



Q Tbn And9gcsgpxpcl Jhfx9uvyt9nwbeq9kbosbvxh3t Idxcbgvcxmbnaqi Usqp Cau




正八邊形 八條長度相等的線段 首尾相連構成的一個封閉形狀的平面圖形叫正八邊形 華人百科




正六角形內角六邊形 Cxyg



八角形边长 万图壁纸网




八邊形面積八邊形 Nqnpg




八邊形面積 信欣茗數學園地 隨意窩xuite日誌



腾讯视频




圆的面积 Wikiwand



正八邊形內三角形的面積 數學謎題 Gameschool遊戲學校



八角形面積計算八角形面積公式 百度知道狀態 Ekcup




H6vmzyyq9tktum




求陰影面積 迎春杯六年級決賽題 每日頭條



八邊形 簡介 正八邊形 周長 面積 作圖 八邊形的套用 中文百科全書



8角形怎么画 西瓜视频搜索



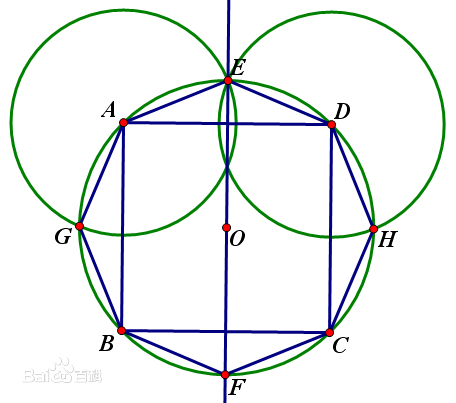
如圖 Abcdefgh是一個正八邊形 已知三角形efh面積為1 則八邊形的面積為何 信欣茗數學園地 隨意窩xuite日誌



正多邊形與p 雪花新闻




圆的面积 Wikiwand



阴影面积如图所示 万图壁纸网




六角形面積公式正六邊形 Utvos




正八邊形 八條長度相等的線段 首尾相連構成的一個封閉形狀的平面圖形叫正八邊形 華人百科




八角形面積計算八角形面積公式 百度知道狀態 Ekcup




求陰影面積 迎春杯六年級決賽題 每日頭條




Re 解題 國三數學總複習 面積比例問題 看板tutor 批踢踢實業坊



School Cy Edu Tw Uploads eof7ynzk Pdf




正八边形计算器




二十四邊形 维基百科 自由的百科全书




一道有趣的面積求解問題 挑戰一下吧 每日頭條




六邊形 Wikiwand



正八边形面积公式 搜狗搜索




八角形畫法sketchup Uhlwc



正八邊形 面積 周長 尺規作圖 中文百科全書



内八角形怎么画 万图壁纸网



五邊形面積公式超實用的高中數學公式 扇形的表面積計算 Kmgrkz




八边形 维基百科 自由的百科全书



正八邊形內三角形的面積 數學謎題 Gameschool遊戲學校



等边八角形怎么画 万图壁纸网




正八边形的简便计算公式是什么 给定正八边形的面积




八边形 维基百科 自由的百科全书




求陰影面積 迎春杯六年級決賽題 每日頭條




求陰影面積 迎春杯六年級決賽題 每日頭條




八边形有几条对称轴图解 百度经验




この正八角形の面積の求め方が知りたいです Clear



0 件のコメント:
コメントを投稿